高校数学Ⅱの参考書に載ってない方程式の解の個数の問題の考え方

507 回閲覧されました
みなさんこんにちは、jonioです。
「程式の解の個数を調べる時だけどどう考えればいいんだろう?その問題にしか使えない考え方じゃなくてどんな問題にも対応できる考え方はないかな?」と思った事はありませんか?
方程式の解の個数の求め方で有名な問題として「\(x^3+x^2+3x+1-a=0\)の解の個数を求めよ。\(a\)を定数とする。」みたいな問題があります。
\(x^3+x^2+3x+1=a\)として\(y=x^3+x^2+3x+1\)と\(y=a\)の共有点の個数を考えますが「とにかくこうする」とやるとこの問題は解けますが他の問題は解けなくなるかもしれません。
だから方程式の解の個数を求める時はどう考えるのかとその考え方を実際の問題に使います。
方程式の解の個数を求める時はこう考える
方程式の解の個数を求める時はグラフを書いて考えます。
理由はグラフを書けば\(x\)軸との共有点の個数が解の個数と分かるからです。
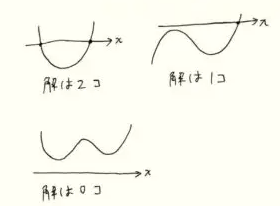
でも\(x^3+x^2+3x+1-a=0\)の解の個数を求める時に\(x\)軸との共有点の個数を考えないで\(x^3+x^2+3x+1=a\)として
\(y=x^3+x^2+3x+1\)と\(y=a\)の共有点の個数を考えますよね?
なぜこの考え方になるかを説明します。
\(x^3+x^2+3x+1-a=0\)で\(y=x^3+x^2+3x+1-a\)として微分して増減表を書いてグラフを書こうとしますができません。
理由は式の中に\(a\)が入っているからで\(a\)がなければグラフを書けますよね。
だから\(x^3+x^2+3x+1=a\)として右辺に\(a\)があるので\(y=x^3+x^2+3x+1\)と\(y=a\)の共有点の個数を考えようとなります。
理由はこれだけですがせっかくなので問題を1問を解きます。
「\(\frac{x^3}{3}-\frac{3}{2}x^2+2x-a=0\)の解の個数が3個になるような定数\(a\)の値の範囲を求めよ。」
\(\frac{x^3}{3}-\frac{3}{2}x^2+2x-a=0\)で\(\frac{x^3}{3}-\frac{3}{2}x^2+2x=a\)として\(y=\frac{x^3}{3}-\frac{3}{2}x^2+2x\)と\(y=a\)の共有点の個数を求めます。
まず\(y=\frac{x^3}{3}-\frac{3}{2}x^2+2x\)を微分して増減表を書きます。
微分して\(y’=x^2-3x+2=(x-1)(x-2)\)となって\(y’=0\)を解くと\(x=1,2\)となります。
増減表は次の通りです。
\(\begin{array}{c|ccccc}
x & \cdots & 1 & \cdots & 2 & \cdots \\
\hline
f'(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & \frac{5}{6} & \searrow & \frac{2}{3} & \nearrow
\end{array}\)
増減表から図を書くと次の通りになります。
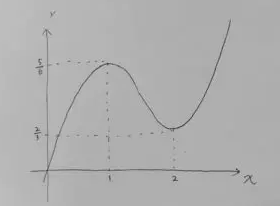
そして\(y=a\)との共有点の個数が3つの時を考えますが\(y=a\)は\(x\)軸に並行な横線で\(\frac{2}{3}\)と\(\frac{5}{6}\)の間にあればいいですよね。
だから\(a\)の範囲は\(\frac{2}{3}\)<\(a\)<\(\frac{5}{6}\)になります。
といった具合に問題を解けますがこの考え方は欠点もあります。
式が\(x^3+x^2+3ax+1-a^2=0\)みたいになったら式「=\(a\)」の形にできないですよね。
こういう時は\(y=x^3+x^2+3ax+1-a^2\)のグラフを書いて\(x\)軸との共有点の個数を考えるしかないです。
具体的に問題を解かないとどうすればいいか分からないと思うので問題を解いてみせます。
「3次方程式\(x^3-3ax+2=0\)が実数解をただ1つもつように定数\(a\)の値の範囲を求めよ。ただし,\(a>0\)とする。」
\(x^3-3ax+2=0\)・・・①から\(\frac{x^3+2}{3x}=a\)とすればこれまでの説明で解く事ができますが左辺が分数関数で数学Ⅲなのでこれで考えるのではなく①のまま考えることにします。
方程式の解の個数を考えるので①の左辺のグラフを考えます。
\(y=x^3-3ax+2\)と置いて微分して増減表を書いてグラフを書きます。
\(y’=3x^2-3a=3(x+\sqrt{a})(x-\sqrt{a})\)
\(y’=0\)を解くと\(x=-\sqrt{a},\sqrt{a}\)
よって増減表は以下の通りです。
\(\begin{array}{c|cc}
x & \cdots & -\sqrt{a} & \cdots & \sqrt{a} & \cdots \\
\hline
f'(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 極大値 & \searrow & 極小値 & \nearrow
\end{array}\)
極大値\(2a\sqrt{a}+2\)は正なので\(y=x^3-3ax+2\)が\(x\)軸と1点で交わるためにはグラフが以下の様になればいいです。
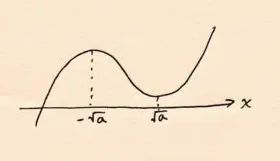
よって極小値\(-2a\sqrt{a}+2\)>\(0\)を解けばいいですが次の様に解きます。
\(-2a\sqrt{a}+2\)>\(0\)
\(a\sqrt{a}\)<\(1\)
\(a^{\frac{3}{2}}\)<\(1^{\frac{3}{2}}\)
両辺を2乗して
\(a^3\)<\(1^3\)
\(a\)<\(1\)
\(a\)>\(0\)より\(0\)<\(a\)<\(1\)となります。
方程式の解の個数の問題は文字定数を分離と学校や塾で習いますが文字定数を分離する理由も知っておかないと難しい問題になった時に対応できなくなるので理由も抑えましょう。
説明を終わります。